题目内容
2.若方程组$\left\{\begin{array}{l}{4x+y=2a}\\{7x+4y=3a-2}\end{array}\right.$的解满足x+y≤-1,求a的取值范围.分析 先解方程组,求得x,y的值,再根据x+y≤-1列出关于a的不等式,求得a的取值范围即可.
解答 解:$\left\{\begin{array}{l}{4x+y=2a①}\\{7x+4y=3a-2②}\end{array}\right.$,
①×4得,16x+4y=8a③,
③-②得,9x=5a+2,
解得x=$\frac{5a+2}{9}$,
把x的值代入①得4×$\frac{5a+2}{9}$+y=2a,
解得y=$\frac{-2a-8}{9}$,
∵x+y≤-1,
∴$\frac{5a+2}{9}$+$\frac{-2a-8}{9}$≤-1,
解得,a≤-1,
∴a的取值范围a≤-1.
点评 本题考查了二元一次方程组的解以及解一元一次不等式,求出方程组中x,y的值是解题的关键.

练习册系列答案
相关题目
17.若a<0,在1、a、1+a、1-a中最大的数是( )
| A. | 1 | B. | a | C. | 1+a | D. | 1-a |
7.△ABC∽△A1B1C1,相似比为$\frac{1}{3}$,△A1B1C1∽△A2B2C2,相似比为$\frac{4}{3}$,则△ABC∽△A2B2C2,其相似比为$\frac{4}{9}$.
12.下列各根式是最简二次根式的是( )
| A. | $\sqrt{15}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{54}$ | D. | $\sqrt{12}$ |
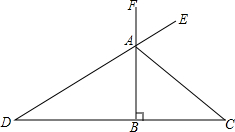 如图,在Rt△ABC中,∠B=90°,AB=6,AC=10,AE为△ABC的外角∠FAC的角平分线,延长EA交CB的延长线于D,求AD的长.
如图,在Rt△ABC中,∠B=90°,AB=6,AC=10,AE为△ABC的外角∠FAC的角平分线,延长EA交CB的延长线于D,求AD的长.