题目内容
已知方程x2+2
x+1=0,两根分别为m和n,则
的值等于( )
| 2 |
| m2+n2+3mn |
| A、9 | B、±3 | C、5 | D、3 |
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到m+n=-2
,mn=1,再利用完全平方公式把原式变形为
,然后利用整体代入的方法计算.
| 2 |
| (m+n)2+mn |
解答:解:根据题意得m+n=-2
,mn=1,
所以原式=
=
=3.
故选D.
| 2 |
所以原式=
| (m+n)2+mn |
(-2
|
故选D.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
如图,已知△ABC的六个元素,则图中甲、乙、丙中能判断和△ABC全等的图形个数是( )


| A、1 | B、2 | C、3 | D、0 |
将下列各数填入适当的括号内:
π,5,-3,
,8.9,19,-
,-3.14,-9,0,2
整数集合:{ …}
分数集合:{ …}
正有理数集合:{ …}
负有理数集合:{ …}
非负数集合:{ …}.
π,5,-3,
| 3 |
| 4 |
| 6 |
| 7 |
| 3 |
| 5 |
整数集合:{ …}
分数集合:{ …}
正有理数集合:{ …}
负有理数集合:{ …}
非负数集合:{ …}.
两个有理数相加,若和为负数,则加数中正数的个数( )
| A、有2个 | B、只有1个 |
| C、至少1个 | D、至多1个 |
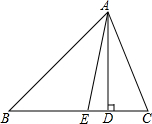 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.