题目内容
13. 如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )
如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )| A. | $\frac{1}{2}$c(a+b-c) | B. | $\frac{1}{2}$c(b+c-a) | C. | $\frac{1}{2}$c(a+c-b) | D. | $\frac{1}{2}$a(b+c-a) |
分析 根据题意求出FN、ME的长与Rt△EAF的斜边上的高代入三角形面积公式计算即可.
解答 解:∵四边形ABCD是矩形,
∴∠EAF=90°,
∵AE=AF=c,
∴∠E=∠F=45°,
∴△FDN与△MBE均为等腰直角三角形,
∴BE=BM=c-a,DF=DN=c-b,
FN=$\sqrt{2}$(c-a),ME=$\sqrt{2}$(c-b),
MN=$\sqrt{2}c$-$\sqrt{2}$(c-a)-$\sqrt{2}$(c-b)=$\sqrt{2}$a+$\sqrt{2}$b-$\sqrt{2}$c
∵Rt△EAF斜边上的高h=$\frac{\sqrt{2}}{2}$c,
∴S△AMN=$\frac{1}{2}$MN•h=$\frac{1}{2}$($\sqrt{2}$a+$\sqrt{2}$b-$\sqrt{2}$c)•$\sqrt{2}$c=$\frac{1}{2}$c(a+b-c).
故:选A
点评 本题考查了矩形的性质以及等腰直角三角形的性质、三角形的面积等知识点,解题的关键是求出FN、ME的长与Rt△EAF的斜边上的高.

练习册系列答案
相关题目
18.5张不同卡片分别写有数字2,3,4,5,6,从中任意取出3张,则这三张卡片上所写的数字可以作为三角形的三边长的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 如图,在等腰△ABC中,AB=AC,BC边上的高AD=3cm,腰AB上的高CE=4cm,则△ABC的周长为6$\sqrt{5}$cm.
如图,在等腰△ABC中,AB=AC,BC边上的高AD=3cm,腰AB上的高CE=4cm,则△ABC的周长为6$\sqrt{5}$cm.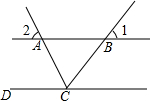 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=65°.
如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=65°.