题目内容
2.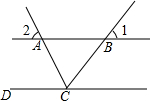 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=65°.
如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=65°.
分析 先根据平行线的性质得∠ABC+∠BCD=180°,根据对顶角相等得∠ABC=∠1=50°,则∠BCD=130°,再利用角平分线定义得到∠ACD=$\frac{1}{2}$∠BCD=65°,然后根据平行线的性质得到∠2的度数.
解答 解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
而∠ABC=∠1=50°,
∴∠BCD=130°,
∵CA平分∠BCD,
∴∠ACD=$\frac{1}{2}$∠BCD=65°,
∵AB∥CD,
∴∠2=∠ACD=65°.
故答案为65°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
13. 如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )
如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )
 如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )
如图,在矩形ABCD中,AB=a,AD=b,分别延长AB至E,AD至F,使得AF=AE=c(b<a<c).连结EF,交BC于M,交CD于N,则△AMN的面积为( )| A. | $\frac{1}{2}$c(a+b-c) | B. | $\frac{1}{2}$c(b+c-a) | C. | $\frac{1}{2}$c(a+c-b) | D. | $\frac{1}{2}$a(b+c-a) |
10.下列各题去括号不正确的是( )
| A. | $x-(2y-\frac{3}{2})=x-2y+\frac{3}{2}$ | B. | $-\frac{1}{2}(2x-6y+4)=-x+3y+4$ | ||
| C. | $(a+\frac{1}{2}b)-2(-\frac{1}{3}c+\frac{2}{7})=a+\frac{1}{2}b+\frac{2}{3}c-\frac{4}{7}$ | D. | m+(-n+4a-3b)=m-n+4a-3b |
11.计算-150+350( )
| A. | 200 | B. | -500 | C. | -200 | D. | 500 |
