题目内容
14. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C不经过池塘可以直接到达点A和B,根据我们所学的几何知识利用尺规作图,至少有两种方法可间接得出A、B两端的距离,请你完成下列作图(不写作法,保留画图痕迹)与填空.
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C不经过池塘可以直接到达点A和B,根据我们所学的几何知识利用尺规作图,至少有两种方法可间接得出A、B两端的距离,请你完成下列作图(不写作法,保留画图痕迹)与填空.方法一:
(1)作图:
(2)填空:量出线段DE的长就是A、B的距离,根据是全等三角形的对应边相等
方法二:
(1)作图:
(2)填空:量出线段DE的长就知道A、B的距离,根据是相似三角形的对应变成比例.
分析 利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答,进而利用相似三角形判定与性质得出答案.
解答 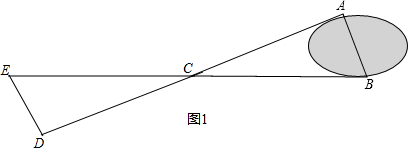 解:方法一:如图1所示:延长AC截取CD=AC,延长BC截取EC=CB,
解:方法一:如图1所示:延长AC截取CD=AC,延长BC截取EC=CB,
量出DE的长就等于AB的长. 这是因为可根据SAS方法判定△ABC≌△DEC利用全等三角形的对应边相等.
故答案为:DE,全等三角形的对应边相等;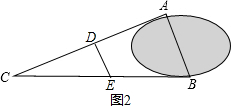
方法二:如图2所示:找到AC的中点D,BC的中点E,
量出DE的长就等于AB的长. 这是因为可根据△ABC∽△DEC,利用相似三角形的对应变成比例.
故答案为:DE,相似三角形的对应变成比例.
点评 本题考查了全等三角形的应用以及相似三角形判定与性质,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
5. 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{5}{3}$ |
19. 如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )
如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )
 如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )
如图,点A、E、F、C在同一条直线上,AD∥BC,BE∥DF,BE的延长线交AD于点G,则下列结论错误的是( )| A. | AG:AD=AE:AF | B. | AG:AD=EG:DF | C. | AG:AD=AE:AC | D. | AD:BC=DF:BE |
6.下列计算正确的是( )
| A. | x3•x4=x12 | B. | (x3)3=x6 | C. | (2ab)2÷(ab)=2ab(ab≠0) | D. | (2a2)3•(-ab)=-8a7b |
3.两个多边形相似的条件是( )
| A. | 对应角相等 | B. | 对应角相等且对应边成比例 | ||
| C. | 对应角相等或对应边成比例 | D. | 对应边成比例 |
4.点A(-1,1)是反比例函数y=$\frac{m}{x}$的图象上一点,则m的值为( )
| A. | 0 | B. | -2 | C. | -1 | D. | 1 |
