题目内容
一条船上午8点在A处望见西南方向有一座灯塔B(如图)，此时测得船和灯塔相距36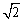
海里，船以每小时20海里的速度向南偏西24°的方向航行到C处，这时望见灯塔在船的正北
方向．(参考数据：sin24°≈0.4，cos24°≈0.9)．
(1)求几点钟船到达C处；
(2)求船到达C处时与灯塔B之间的距离．
（1）延长CB与AD交于点E．∴∠AEB=90°，∵∠BAE=45°，AB=36
。∴BE=AE=36．根据题意得：∠C=24°，sin24°=
∴AC=90．90÷20=4.5，所以12点30分到达C处；
（2）在直角三角形ACE中，cos24°=
，即cos24°=
，BC=45．所以船到C处时，船和灯塔的距离是45海里．
练习册系列答案
相关题目
；那么
等于（ ）
B、 
C、
D、
,AE＝3,求AF的长.
。
向左平移2个单位，再向上平移1个单位，所得到的抛物线的解析式为：
B.
D.
的图象如图所示，若一元二次方程
有实数根，则m的最小值为：