题目内容
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. (4分+6分)
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
 |
解:(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=
∵△ADF∽△DEC
∴  ∴
∴ ……9分 AF=
……9分 AF=

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目


 ,0,
,0, 的极差3,则整数
的极差3,则整数 有意义的自变量x的取值范围是( )
有意义的自变量x的取值范围是( ) ;B.x≠
;B.x≠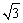 )cm2;
)cm2;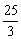
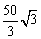 )cm2
)cm2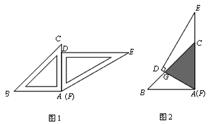
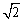 海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北
海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北