题目内容
2.△ABC中,∠A=60°,AB与AC这两边上的高所在的直线相交于点H,若△ABC不是直角三角形,则∠BHC=120或60(度).分析 根据四边形的内角和,可得∠DHE,根据对顶角的性质,可得答案.
解答 解:①如图:当△ABC是锐角三角形时, ,
,
由BE⊥AC,CD⊥AB,得
∠HDA=∠HEA=90°.
由四边形的内角和,得
∠DHE=360°-∠A-∠ADH-∠AEH=360°-60°-90°-90°=120°,
由对顶角相等,得
∠BHC=∠DHE=120°,
②△ABC是钝角三角形时,不妨设∠ABC>90°,如图,
∵∠A=60°,∠AEB=∠BDH=90°,∠ABE=∠DBH,
∴∠H=∠A=60°,
故答案为:120或60.
点评 本题考查了三角形的内角和定理,利用了四边形内角和,对顶角的性质.

练习册系列答案
相关题目
10.如果|x|=3,则|x+1|的值是( )
| A. | 4 | B. | 2 | C. | 4或2 | D. | 以上都不对 |
12.下列乘法中,能应用平方差公式的是( )
| A. | (x-y)(y-x) | B. | (2x-3y)(3x+2y) | C. | (-x-y)(x+y) | D. | (-2x-3y)(3y-2x) |
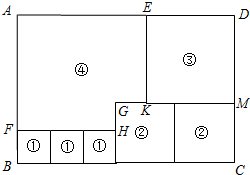 如图,用3个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个长方形ABCD.若GH=2cm,GK=2cm,设BF=x cm.
如图,用3个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个长方形ABCD.若GH=2cm,GK=2cm,设BF=x cm. 观察如图有※组成的图案和下面的算式,解答问题:
观察如图有※组成的图案和下面的算式,解答问题: