题目内容
16.计算:$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$.分析 设$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$=x,平方得6-$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$=x2,可得方程6-x=x2,解方程即可求解.
解答 解:设$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$=x,
平方得6-$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$=x2,
6-x=x2,
(x+3)(x-2)=0,
x1=-3,x2=2,
∵$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$>0,
∴x=2,
∴$\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-\sqrt{6-…}}}}}$=2.
点评 考查了实数的运算,本题关键是利用换元法得到方程6-x=x2,再解方程求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.由一列数按如下规律排列:-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{3}}{4}$,$\frac{1}{4}$,-$\frac{\sqrt{5}}{16}$,-$\frac{\sqrt{6}}{32}$,-$\frac{\sqrt{7}}{64}$,则第2017个数是( )
| A. | $\frac{\sqrt{2017}}{{2}^{2016}}$ | B. | -$\frac{\sqrt{2017}}{{2}^{2016}}$ | C. | $\frac{\sqrt{2018}}{{2}^{2017}}$ | D. | -$\frac{\sqrt{2018}}{{2}^{2017}}$ |
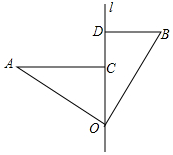 如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A,B两点作AC⊥l,BD⊥l,垂足分别为点C,D.求证:AC=OD.
如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A,B两点作AC⊥l,BD⊥l,垂足分别为点C,D.求证:AC=OD.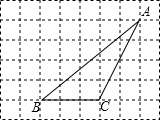 如图所示,在边长为1个单位长度的正方形网格中,作出△ABC的边BC上的高,并计算△ABC的面积.
如图所示,在边长为1个单位长度的正方形网格中,作出△ABC的边BC上的高,并计算△ABC的面积. 如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.
如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.