题目内容
已知a是方程x2-2006x-1=0的根，试判断代数式
+
的值是无理数、分数还是整数，并说明理由．
| a2-2006a |
| 2006a |
| a2-1 |
考点：一元二次方程的解,二次根式的性质与化简
专题：
分析：把x=a代入得出方程，求出a2-2006a=1，a2-1=2006a，再代入即可求出答案．
解答：解：代数式
+
的值是整数，
理由是：∵a是方程x2-2006x-1=0的根，
∴a2-2006a-1=0，
∴a2-2006a=1，a2-1=2006a，
∴
+
=
+
=1+1
=2，
即代数式
+
的值是整数．
| a2-2006a |
| 2006a |
| a2-1 |
理由是：∵a是方程x2-2006x-1=0的根，
∴a2-2006a-1=0，
∴a2-2006a=1，a2-1=2006a，
∴
| a2-2006a |
| 2006a |
| a2-1 |
=
| 1 |
| 2006a |
| 2006a |
=1+1
=2，
即代数式
| a2-2006a |
| 2006a |
| a2-1 |
点评：本题考查了一元二次方程的解，二次根式的性质的应用，解此题的关键是求出a2-2006a=1，a2-1=2006a．
练习册系列答案
相关题目
在5×5的方格中，每个方格的面积都是1，试在方格中画一个面积为8的正方形．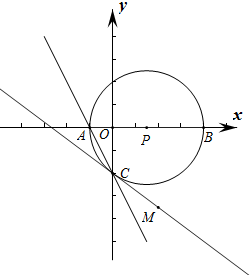
如图，在直角坐标中，坐标原点为O，A点的坐标为（-1，0），B点的坐标为（4，0），以AB的中点P为圆心作⊙P与y轴的负半轴交于点C．