题目内容

13．抛物线y=3x2+6x-12的对称轴是（　　）
A．x=-1B．x=1C．x=-2D．x=2

分析 首先将y=3x2+6x-12配方成顶点式y=a（x-m）2+n的形式，即可求出对称轴：直线x=n．

解答 解：∵y=3x2+6x-12=3（x+1）2-15，
∴对称轴是直线x=-1．
故选：A．

点评 此题考查二次函数的性质，能正确配方成顶点式是解决问题的关键．

练习册系列答案
相关题目
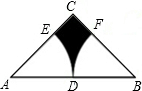3．如图，Rt△ABC中，∠C=90°，AC=BC=4，点D是线段AB的中点，分别以点A，B为圆心，AD为半径画弧，分别交AC，BC于点E，F．则阴影部分面积为8-2π（结果保留π）．
4．二次函数y=（k-2）x2+k2-4的图象经过原点，则k的值是-2．
1．已知点A与点（-4，5）关于y轴对称，则A点坐标是（　　）
A．（4，-5）B．（-4，-5）C．（-5，-4）D．（4，5）
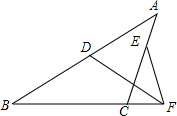8．如图，在△ABC中，F为BC延长线一点，D为AB上一点，且DB=DF，E为AC上一点，且EC=EF，∠A=40°，∠DFE的度数为（　　）
A．30B．35C．40D．50
18．下列函数中①y=3x+1；②y=4x2-3x；③y=$\frac{4}{{x}^{2}}$+x2；④y=5-2x2，是二次函数的有（　　）
A．②B．②③④C．②③D．②④
5．对于实数a、b，定义一种运算“?”为：a?b=$\frac{（a-1）^{2}}{a}$-ab．有下列命题：①1?（-3）=3； ②a?b=b?a；③方程（x-$\frac{1}{2}$）?1=0的解为x=$\frac{1}{2}$；其中正确命题的序号是①．（把所有正确命题的序号都填上）．
2．如图，已知A、B两点分别为（0，1）（3，5），P是x轴上的一个动点，当△ABP的周长最小时，P点的坐标为（　　）
A．（0，0）B．（3，0）C．（0，5，0）D．（1.5，0）
3．下列等式正确的是（　　）
A．1+（-3）=$\frac{1}{3}$B．-（-1）=-1C．|-2|=2D．（-2）×3=6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网