题目内容
13．若函数y=$\frac{{x}^{2}+3x+5}{{x}^{2}+1}$的最大值是M，最小值是m，则M-m=5．分析 根据题意把原式变形，根据方程有实根得到△＞0，求出y的范围，得到y的最大值和最小值，计算即可．
解答 解：∵y=$\frac{{x}^{2}+3x+5}{{x}^{2}+1}$，
∴y（x2+1）=x2+3x+5，
∴（1-y）x2+3x+5-0，
△=9-4（1-y）×（5-y）≥0，
即4y2-24y+11≤0，
则（2y-1）（2y-11）≤0，
∴$\frac{1}{2}$≤x≤$\frac{11}{2}$，
∴M=$\frac{11}{2}$，m=$\frac{1}{2}$，
M-m=5，
故答案为：5．
点评 本题考查的是一元二次方程根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
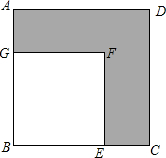如图，工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG，若阴影部分面积为240mm2，AB=2x+8，BE=2x-4，求大正方形的边长．
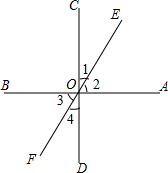如图所示，三条直线AB，CD，EF都经过点O，且∠AOC=90°
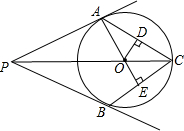从⊙O外一点P引⊙O的切线PA、PB，切点分别为A、B两点，连结PO并延长PO交⊙O于点C，连接CA，CB，OD⊥AC，OE⊥CB，垂足分别为D、E，求证：OD=OE．