题目内容
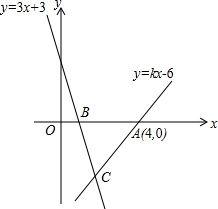 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.(1)求k的值;
(2)求点C的坐标;
(3)求△ABC的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)直接把点A代入y=kx-6求得答案即可;
(2)利用直线y=-3x+3求得点B坐标,进一步与直线y=
x-6建立方程组求得x、y的数值得出点C的坐标;
(3)利用点的坐标求得AB,根据三角形的面积计算公式求得答案即可.
(2)利用直线y=-3x+3求得点B坐标,进一步与直线y=
| 3 |
| 2 |
(3)利用点的坐标求得AB,根据三角形的面积计算公式求得答案即可.
解答: 解:(1)∵直线y=kx-6经过点A(4,0),
解:(1)∵直线y=kx-6经过点A(4,0),
∴4k-6=0,即k=
;
(2)∵直线y=-3x+3与x轴交于点B,根据在
x轴上的点纵坐标y=0,在y轴上的点横坐标x=0.
∴-3x+3=0,解得x=1.点B坐标为(1,0).
由于两直线交于点C,所以有
,
解得
.
∴点C坐标为(2,-3).
(3)△ABC面积为:
×|AB|×|-3|=
×|3|×|-3|=
.
答:△ABC的面积为
.
 解:(1)∵直线y=kx-6经过点A(4,0),
解:(1)∵直线y=kx-6经过点A(4,0),∴4k-6=0,即k=
| 3 |
| 2 |
(2)∵直线y=-3x+3与x轴交于点B,根据在
x轴上的点纵坐标y=0,在y轴上的点横坐标x=0.
∴-3x+3=0,解得x=1.点B坐标为(1,0).
由于两直线交于点C,所以有
|
解得
|
∴点C坐标为(2,-3).
(3)△ABC面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
答:△ABC的面积为
| 9 |
| 2 |
点评:此题考查待定系数法求函数解析式,两条直线相交的问题,以及利用坐标求图形的面积,数形结合,解决问题.

练习册系列答案
相关题目
下列几何体中,属于圆锥的是( )
A、 |
B、 |
C、 |
D、 |
 实数a,b在数轴上的对应点如图所示,则下列不等式中正确的是( )
实数a,b在数轴上的对应点如图所示,则下列不等式中正确的是( )| A、a+b<0 | ||
| B、b-a<0 | ||
| C、ab<0 | ||
D、
|
 如图所示,用5个小正方体搭成的立体图形,请你从正面、左面、上面观察这个几何体,分别画出你所看到的几何体的形状图.
如图所示,用5个小正方体搭成的立体图形,请你从正面、左面、上面观察这个几何体,分别画出你所看到的几何体的形状图.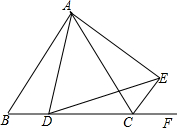 如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.
如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由. (1)在数轴上表示下列各数
(1)在数轴上表示下列各数