题目内容
已知抛物线C：y＝ax2＋bx＋c(a＜0)过原点，与x轴的另一个交点为B(4，0)，A为抛物线C的顶点．
(1)如图，若∠AOB＝60°，求抛物线C的解析式；
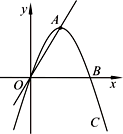
(2)如图，若直线OA的解析式为y＝x，将抛物线C绕原点O旋转180°得到抛物线
，求抛物线C、的解析式；
(3)在(2)的条件下，设
为抛物线的顶点，求抛物线C或上使得PB＝P
的点P的坐标．
解析：
|
(1)连接AB．∵A点是抛物线C的顶点，且C交x轴于O、B，∴AO＝AB， 又∵∠AOB＝60°，∴△ABO是等边三角形 1分 过A作AD⊥x轴于D，在Rt△OAD中，易求出OD＝2，AD＝ ∴顶点A的坐标为(2， 设抛物线C的解析式为 ∴抛物线C的解析式为 (2)过A作AE⊥OB于E， ∵抛物线C： 又∵直线OA的解析式为y＝x，∴AE＝OE＝2，∴点A的坐标为(2，2) 4分 将A、B、O的坐标代入 ∴抛物线C的解析式为 又∵抛物线C、 (3)作 由前可知，抛物线 作MH⊥x轴于H，易证△MHN∽△BHM，则 ∴ ∵直线l过点M(1，－1)、N( 解 ∴在抛物线C上存在两点使得 P1( 解 ∴在抛物线 P3(－5＋ (用两点间的距离公式解决亦可) |
，
) 2分
(a≠0)，将O(0，0)的坐标代入，可求a＝
，
3分
过原点和B(4，0)，顶点为A，∴OE＝
OB＝2，
中，易求a＝
，
5分
关于原点对称，∴抛物线
的解析式为
6分
B的垂直平分线l，分别交
B、x轴于M、N(n，0)，
，即
，
，即N点的坐标为(
，0)．
8分
得，
．
，其坐标分别为
，
)，P2(
，
) 9分
得，
．
上也存在两点使得
，17－3
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案如图，已知抛物线P：y＝ax2＋bx＋c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
|
x |
… |
－3 |
－2 |
1 |
2 |
… |
|
y |
… |
－ |
－4 |
－ |
0 |
… |
(1)
求A、B、C三点的坐标；(2)
若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；(3)
当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围．
与直线y＝2x交于点O(0，0)，A(a，12)，点B是抛物线上O，A之间的一个动点，过点B分别作x轴、y轴的平行线与直线OA交于点C，E．
与直线y＝x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴．
，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．
．
