Question

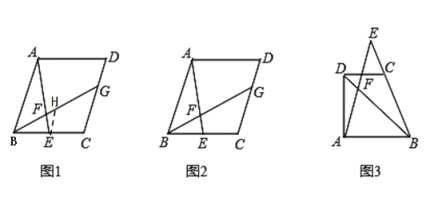
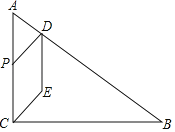
【题目】如图，在Rt△ABC中，∠C＝90°，BC＝2AC，D，E，F分别为BC，AC，AB边上的点，BF＝3AF，∠DFE＝90°，若△BDF与△FEA的面积比为3：2，则△CDE与△DEF的面积比为_____．

Answer 1

【答案】5：12

【解析】

过点D、E分别作AB的垂线DG、EH，由BF＝3AF及△BDF与△FEA的面积比为3：2，可求得EH和DG的数量关系，设FG＝x，DG＝a，则BG＝2a，AH＝a，EH＝2a，先证明△DFG∽△FEH，用x和a表示出FH，再根据BF＝3AF，列出方程，用含a的式子表示出x，然后用含a的式子表示出相关线段，进而表示出△CDE与△DEF的面积，两者相比即可得解．

解：如图，过点D、E分别作AB的垂线DG、EH交AB于点G,H

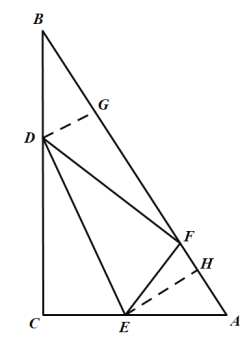
∵BF＝3AF，△BDF与△FEA的面积比为3：2，

∴

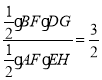
∴EH＝2DG

∵∠C＝90°，BC＝2AC

∴tan∠B＝

∴BG＝2DG

设FG＝x，DG＝a，则BG＝2a，AH＝a，EH＝2a

∴AE＝＝a

∵∠DFE＝90°，

∴∠DFG+∠EFH＝90°

又∵∠FEH+∠EFH＝90°

∴∠DFG＝∠FEH

又∵∠FGD＝∠EHF＝90°

∴△DFG∽△FEH

∴＝

∴＝

∴FH＝

∵BF＝3AF

∴2a+x＝3（a+）

整理得：x2﹣ax﹣6a2＝0

解得：x＝3a或x＝﹣2a（舍）

∴FH＝，BA＝4AF＝4（a+）＝

∵∠C＝90°，BC＝2AC

∴AC：BC：AB＝1：2：

∴AC＝＝，BC＝2AC＝

由勾股定理得：DF＝＝＝a，

EF＝＝＝

∴S△DEF＝DFEF＝×a×＝

∵AC＝，BC＝，AE＝a

CE＝AC﹣AE＝，CD＝CB﹣BD＝﹣＝

∴S△CDE＝CECD＝××＝

∴S△CDE：S△DEF＝：＝5：12

故答案为：5：12．