题目内容
在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为 ．
考点：列表法与树状图法
专题：计算题
分析：列表得出所有等可能的情况数，找出两次摸取的小球标号都是1的情况数，即可求出所求的概率．
解答：解：列表如下：
所有等可能的情况有16种，其中两次摸取的小球标号都是1的情况有1种，
则P=
．
故答案为：
| 1 | 2 | 3 | 4 | |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
则P=
| 1 |
| 16 |
故答案为：
| 1 |
| 16 |
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
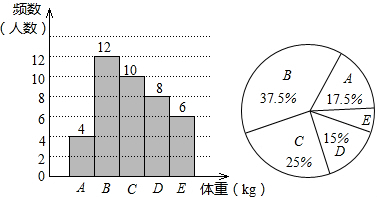进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
如图，直线AB，CD被直线EF所截，若AB∥CD，∠EGF=65°，GE平分∠AEF，则∠EFG=
如图，若边长为1的正方形OABC的顶点B在反比例函数y=
如图是小华在3月8日“妇女节”送给她妈妈的礼盒，图中所示礼盒的俯视图是（ ）
已知：如图，△ABC中，点O是AC上的一动点，过点O作直线MN∥AC，设MN交∠BCA的平分线于点E，交∠BCA的外角∠ACG的平分线于点F，连接AE、AF．