题目内容
不解方程，判别方程x2+4x+4=0的根的情况是（ ）
| A、有两个相等的实数根 |
| B、有两个互为相反数的实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
考点：根的判别式
专题：
分析：先计算△=b2-4ac的值，得到△=0，然后根据△的意义判断即可．
解答：解：∵△=42-4×1×4=0，
∴方程有两个相等的实数根．
故选A．
∴方程有两个相等的实数根．
故选A．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下列代数式中，单项式共有（ ）
-2ab，
，x+y，x2+y2，-1，
ab2c3．
-2ab，
| 3 |
| x |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
现给出以下几个命题：（1）经过三点一定可以作圆；（2）相等的圆心角所对的弧相等；（3）垂直于弦的直线平分这条弦并且平分弦所对的两条弧；（4）钝角三角形的外接圆圆心在三角形外面；其中真命题的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
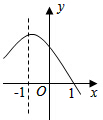抛物线y=ax2+bx+c的对称轴为直线x=-1，与x轴的一个交点为（1，0），部分图象如图所示，若y＞0，则x的取值范围是（ ）| A、-4＜x＜1 |
| B、-3＜x＜1 |
| C、x＜-4或x＞1 |
| D、x＜-3或x＞1 |
-4n+1=（-4）n+1成立的条件是（ ）
| A、n为奇数 | B、n是正整数 |
| C、n是偶数 | D、n是负数 |
已知线段AB=4cm，在直线AB上画线段BC=2cm，则线段AC的长为（ ）
| A、5cm和2cm |
| B、6cm和5cm |
| C、2cm和3cm |
| D、6cm和2cm |
x克盐溶解在a克水中，取这种盐水m克，其中含盐（ ）克．
A、
| ||
B、
| ||
C、
| ||
D、
|