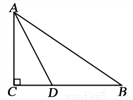
题目内容
如图,二次函数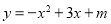 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


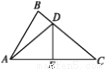

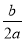 ,
,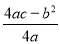 )
)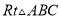 中,
中, 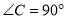 ,AD平分
,AD平分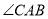 ,AC=6,BC=8,则CD的长为
,AC=6,BC=8,则CD的长为