题目内容
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
考点:一元一次不等式组的应用
专题:
分析:(1)设建设A型x套,B型(40-x)套,然后根据投入资金不超过200万元,又不低于198万元列出不等式组,求出不等式组的解集,再根据x是正整数解答;
(2)设总投资W元,建设A型x套,B型(40-x)套,然后根据总投资等于A、B两个型号的投资之和列式函数关系式,再根据一次函数的增减性解答.
(2)设总投资W元,建设A型x套,B型(40-x)套,然后根据总投资等于A、B两个型号的投资之和列式函数关系式,再根据一次函数的增减性解答.
解答:解:(1)设建设A型x套,则B型(40-x)套,
根据题意得
,
解不等式①得,x≥15,
解不等式②得,x≤20,
所以不等式组的解集是15≤x≤20,
∵x为正整数,
∴x=15、16、17、18、19、20,
答:共有6种方案;
(2)设总投资W万元,建设A型x套,则B型(40-x)套,则
W=5.2x+4.8×(40-x)=0.4x+192,
∵0.4>0,
∴W随x的增大而增大,
∴当x=15时,W最小,此时W最小=0.4×15+192=198万元.
答:当建设A型15套时,投入资金最少,最少资金是198万元.
根据题意得
|
解不等式①得,x≥15,
解不等式②得,x≤20,
所以不等式组的解集是15≤x≤20,
∵x为正整数,
∴x=15、16、17、18、19、20,
答:共有6种方案;
(2)设总投资W万元,建设A型x套,则B型(40-x)套,则
W=5.2x+4.8×(40-x)=0.4x+192,
∵0.4>0,
∴W随x的增大而增大,
∴当x=15时,W最小,此时W最小=0.4×15+192=198万元.
答:当建设A型15套时,投入资金最少,最少资金是198万元.
点评:本题考查了一次函数的应用,一元一次不等式组的应用,读懂题目信息,理清题中不等量关系,列出不等式组是解题的关键,(2)利用一次函数的增减性求最值要注意自变量的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
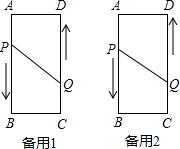 如图,长方形ABCD(长方形的对边相等,每个角都是90°),AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2厘米/秒的速度向终点B移动,点Q以1厘米/秒的速度向D移动,当有一点到达终点时,另一点也停止运动.设运动的时间为t,问:
如图,长方形ABCD(长方形的对边相等,每个角都是90°),AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2厘米/秒的速度向终点B移动,点Q以1厘米/秒的速度向D移动,当有一点到达终点时,另一点也停止运动.设运动的时间为t,问: 如图,A,B两点分别在x轴,y轴的正半轴上,且OA=4,OB=2.
如图,A,B两点分别在x轴,y轴的正半轴上,且OA=4,OB=2. 如图,对称轴为直线x=3得抛物线经过A(0,3)、B(2,0)两点,此抛物线与x轴的另一个交点为C.
如图,对称轴为直线x=3得抛物线经过A(0,3)、B(2,0)两点,此抛物线与x轴的另一个交点为C. 如图:AB∥CD,若∠ABE=130°,∠CDE=150°,则∠BED=
如图:AB∥CD,若∠ABE=130°,∠CDE=150°,则∠BED=