题目内容
12.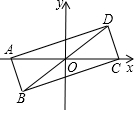 如图,在直角坐标平面内,矩形ABCD的对角线AC、BD交于原点O,且点A、C都在x轴上,点D的坐标为(4,3),那么点C的坐标为(5,0).
如图,在直角坐标平面内,矩形ABCD的对角线AC、BD交于原点O,且点A、C都在x轴上,点D的坐标为(4,3),那么点C的坐标为(5,0).
分析 过点D,作DE⊥OC于点E,利用勾股定理可求出OD的长,根据矩形的性质可得OD=OC,进而可求出点C的坐标.
解答 解:
过点D,作DE⊥OC于点E,
∵点D的坐标为(4,3),
∴OE=4,DE=3,
∴OD=$\sqrt{O{E}^{2}+E{D}^{2}}$=5,
∵四边形ABCD是矩形,
∴OD=OC=$\frac{1}{2}$AC=$\frac{1}{2}$BD,
∴点C的坐标为(5,0),
故答案为:(5,0).
点评 本题考查了矩形的性质以及勾股定理的运用,求出OC的长是解题的关键.

练习册系列答案
相关题目
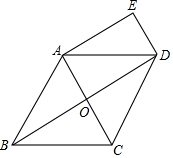 如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.