题目内容
 (1)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=40°,求∠BOC的度数;
(1)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=40°,求∠BOC的度数;(2)若把(1)中∠A=40°这个条件去掉,试探究∠BOC和∠A之间有怎样的数量关系?请写出这个数量关系的推理过程.
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解;
(2)思路同(1)求解即可.
(2)思路同(1)求解即可.
解答: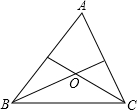 解:(1)∵∠A=40°,
解:(1)∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×140°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°;
(2)∠BOC=90°+
∠A.
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-∠A),
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
(180°-∠A)=90°+
∠A,
即∠BOC=90°+
∠A.
 解:(1)∵∠A=40°,
解:(1)∵∠A=40°,∴∠ABC+∠ACB=180°-40°=140°,
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°;
(2)∠BOC=90°+
| 1 |
| 2 |
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠BOC=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
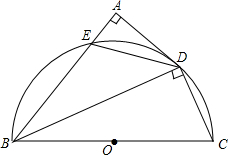 如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4
如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4  如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明CD∥EF.
如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明CD∥EF. 如图,在△ABC中,AB=AC,AD⊥BC于点D,E是AD的中点,CE交AD边于点F,DG∥CF,交AB边于G.若AB=6,求线段AF的长.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E是AD的中点,CE交AD边于点F,DG∥CF,交AB边于G.若AB=6,求线段AF的长. 如图,∠A+∠B+∠C+∠D+∠E=
如图,∠A+∠B+∠C+∠D+∠E=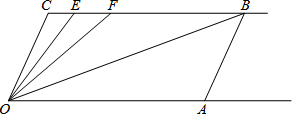 已知:如图,射线CB∥OA,∠C=∠OAB=120°,OE平分∠COF 交BC于点E,F在BC上,且满足OB平分∠AOF.
已知:如图,射线CB∥OA,∠C=∠OAB=120°,OE平分∠COF 交BC于点E,F在BC上,且满足OB平分∠AOF.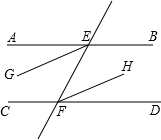 如图所示,AB∥CD、EF分别交AB,CD于E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.
如图所示,AB∥CD、EF分别交AB,CD于E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.