题目内容
9. 三角形ABO在平面直角坐标系上如图放置,已知点A(0,10),点B在x轴上,点C在OB上,且AO+OC=AB+BC,BC=2.
三角形ABO在平面直角坐标系上如图放置,已知点A(0,10),点B在x轴上,点C在OB上,且AO+OC=AB+BC,BC=2.(1)求点C的坐标.
(2)过点C作直线L,将三角形ABO的面积两等分,求直线L的解析式.
分析 (1)设点C的坐标为(x,0),可得OA=10,OB=x+2,AB=8+x,根据勾股定理可得关于x的方程,解之可得;
(2)设直线L与y轴的交点为D,根据S△COD=$\frac{1}{2}$S△AOB可得OD的长,即可知点D的坐标,继而待定系数法可求得直线L的解析式.
解答 解:(1)设点C的坐标为(x,0)
∵点A(0,10),点B在x轴上,点C在OB上,且AO+OC=AB+BC,BC=2,
∴OA=10,OB=x+2,AB=8+x,
∴102+(x+2)2=(8+x)2,
解得,x=$\frac{10}{3}$,
即点C的坐标是($\frac{10}{3}$,0);
(2)设直线L与y轴的交点为D,如图所示,
∵OA=10,OB=$\frac{10}{3}+2=\frac{16}{3}$,OC=$\frac{10}{3}$,过点C作直线L,将三角形ABO的面积两等分,
∴$\frac{OC•OD}{2}=\frac{1}{2}×\frac{OB•OA}{2}$,
即$\frac{\frac{10}{3}×OD}{2}=\frac{1}{2}×\frac{\frac{16}{3}×10}{2}$,
解得,OD=8,
则点D(0,8),
设过点C($\frac{10}{3}$,0)、点D(0,8)的直线L的解析式为:y=kx+b,
$\left\{\begin{array}{l}{\frac{10}{3}k+b=0}\\{b=8}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{12}{5}}\\{b=8}\end{array}\right.$,
即直线L的解析式是y=$-\frac{12}{5}x+8$.
点评 本题主要考查勾股定理和待定系数法求一次函数解析式,根据两三角形面积间关系求得点D的坐标是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 若y-4=8,则y=8-4 | |
| B. | 若2(2x-3)=2,则4x-6=2 | |
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | |
| D. | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1,则去分母得2-3(t-1)=1 |
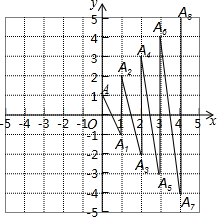 如图在平面直角坐标系上有一点A(0,1),点A第一次跳动至点A1(1,-1),第二次由点 A1跳到点A2(1,2),第三次由点A2跳到A3(2,-2)…由此规律跳动下去,第80次跳到点A80的坐标是( )
如图在平面直角坐标系上有一点A(0,1),点A第一次跳动至点A1(1,-1),第二次由点 A1跳到点A2(1,2),第三次由点A2跳到A3(2,-2)…由此规律跳动下去,第80次跳到点A80的坐标是( )| A. | (40,40) | B. | (41,40) | C. | (40,41) | D. | (41,41) |
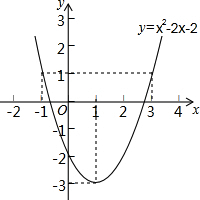 函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )
函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )| A. | -1≤x≤3 | B. | -1<x<3 | C. | x<-1或x>3 | D. | x≤-1或x≥3 |

