题目内容
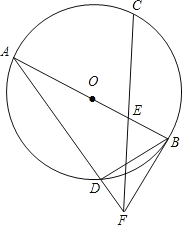
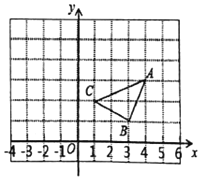
【题目】如图,Rt△ABC中,∠BAC=90°,AB=3,AC=6![]() ,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为_____.
,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为_____.
【答案】![]()
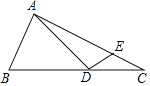
【解析】如图,作A关于BC的对称点A',连接AA',交BC于F,过A'作AE⊥AC于E,交BC于D,则AD=A'D,此时AD+DE的值最小,就是A'E的长,根据相似三角形对应边的比可得结论.
如图,作A关于BC的对称点A',连接AA',交BC于F,过A'作AE⊥AC于E,交BC于D,则AD=A'D,此时AD+DE的值最小,就是A'E的长;
Rt△ABC中,∠BAC=90°,AB=3,AC=6![]() ,
,
∴BC=![]() =9,
=9,
S△ABC=![]() ABAC=
ABAC=![]() BCAF,
BCAF,
∴3×6![]() =9AF,
=9AF,
AF=2![]() ,
,
∴AA'=2AF=4![]() ,
,
∵∠A'FD=∠DEC=90°,∠A'DF=∠CDE,
∴∠A'=∠C,
∵∠AEA'=∠BAC=90°,
∴△AEA'∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴A'E=![]() ,
,
即AD+DE的最小值是![]() ,
,
故答案为:![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目