题目内容
如图,线段AD=5,⊙A的半径为1,C为⊙A上一动点,CD的垂直平分线 分别交CD,AD于点E,B,连接BC,AC,构成△ABC,设AB=x.
分别交CD,AD于点E,B,连接BC,AC,构成△ABC,设AB=x.(1)求x的取值范围;
(2)若△ABC为直角三角形,则x=
(3)设△ABC的面积的平方为W,求W的最大值.
分析:(1)由AD=5,AB=x,BE垂直平分CD,可得BC=BD=5-x,又由,⊙A的半径为1,根据三角形三边关系,即可求得x的取值范围;
(2)分别从若AB是斜边与BC是斜边去分析,利用勾股定理的知识,借助于方程即可求得x的值;
(3)在△ABC中,作CF⊥AB于F,设CF=h,AF=m,则W=(
xh)2=
x2h2,由AC2-AF2=BC2-BF2,则1-m2=(5-x)2-(x-m)2,分别从2.4<x<3时与2<x≤2.4去分析,即可求得答案.
(2)分别从若AB是斜边与BC是斜边去分析,利用勾股定理的知识,借助于方程即可求得x的值;
(3)在△ABC中,作CF⊥AB于F,设CF=h,AF=m,则W=(
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:(1)∵AD=5,AB=x,BE垂直平分CD,
∴BC=BD=5-x,在△ABC中,AC=1,
∴(5-x)-1<x<1+(5-x),
解得:2<x<3;
(2)∵△ABC为直角三角形,
若AB是斜边,则AB2=AC2+BC2,
即x2=(5-x)2+1,
∴x=2.6;
若BC是斜边,则BC2=AB2+AC2,
即(5-x)2=x2+1,
∴x=2.4.
故答案为:2.4或2.6.
(3)在△ABC中,作CF⊥AB于F,
设CF=h,AF=m,则W=(
xh)2=
x2h2,
①如图,当2.4<x<3时,AC2-AF2=BC2-BF2,则1-m2=(5-x)2-(x-m)2,
得:m=
,
∴h2=1-m2=
,
∴W=
x2h2=-6x2+30x-36,
即W=-6(x-
)2+
,
当x=2.5时(满足2.4<x<3),W取最大值1.5;
②当2<x≤2.4时,同理可得:W=-6x2+30x-36=-6(x-
)2+
,
当x=2.4时,W取最大值1.44<1.5,
综合①②得,W的最大值为1.5.
∴BC=BD=5-x,在△ABC中,AC=1,
∴(5-x)-1<x<1+(5-x),
解得:2<x<3;
(2)∵△ABC为直角三角形,
若AB是斜边,则AB2=AC2+BC2,
即x2=(5-x)2+1,
∴x=2.6;
若BC是斜边,则BC2=AB2+AC2,
即(5-x)2=x2+1,
∴x=2.4.
故答案为:2.4或2.6.

(3)在△ABC中,作CF⊥AB于F,
设CF=h,AF=m,则W=(
| 1 |
| 2 |
| 1 |
| 4 |
①如图,当2.4<x<3时,AC2-AF2=BC2-BF2,则1-m2=(5-x)2-(x-m)2,
得:m=
| 5x-12 |
| x |
∴h2=1-m2=
| -24x2+120x-144 |
| x2 |
∴W=
| 1 |
| 4 |
即W=-6(x-
| 5 |
| 2 |
| 3 |
| 2 |
当x=2.5时(满足2.4<x<3),W取最大值1.5;
②当2<x≤2.4时,同理可得:W=-6x2+30x-36=-6(x-
| 5 |
| 2 |
| 3 |
| 2 |
当x=2.4时,W取最大值1.44<1.5,
综合①②得,W的最大值为1.5.
点评:此题考查了三角形三边关系,线段垂直平分线的性质,直角三角形的性质以及二次函数的最值问题等知识.此题综合性很强,难度适中,解题的关键是注意数形结合与分类讨论思想的应用.

练习册系列答案
相关题目
 21、如图,线段AD,AB,BC和EF的长分别为1.8,3,2.5和2,记闭合折线AEBCFD的面积为S,则下面四个选择中正确的是( )
21、如图,线段AD,AB,BC和EF的长分别为1.8,3,2.5和2,记闭合折线AEBCFD的面积为S,则下面四个选择中正确的是( )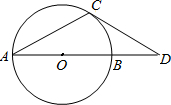 如图,线段AD经过圆心O,交⊙O于点A、B,∠CAB=∠D=30°,边DC交⊙O于点C,CD是⊙O的切线吗?为什么?
如图,线段AD经过圆心O,交⊙O于点A、B,∠CAB=∠D=30°,边DC交⊙O于点C,CD是⊙O的切线吗?为什么? 如图:线段AD与BC相交于点O,且AC=BD,AD=BC.
如图:线段AD与BC相交于点O,且AC=BD,AD=BC. 如图,线段AD,BC相交于点O,若OA=OB,为了用“ASA”判定△AOC≌△BOD,则应补充条件( )
如图,线段AD,BC相交于点O,若OA=OB,为了用“ASA”判定△AOC≌△BOD,则应补充条件( ) 如图,线段AD=5cm,BC=8cm,点D是AC的中点,则BD的长为
如图,线段AD=5cm,BC=8cm,点D是AC的中点,则BD的长为