题目内容
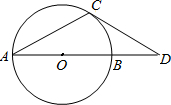如图，线段AD经过圆心O，交⊙O于点A、B，∠CAB=∠D=30°，边DC交⊙O于点C，CD是⊙O的切线吗？为什么？分析：连接OC，由∠CAB=∠D=30°可知∠COD=60°，在△OCD中由三角形内角和定理即可得出∠OCD的度数，进而得出结论．
解答：
证明：连接OC，
∵∠CAB=∠D=30°，
∴∠COD=60°，
∴∠OCD=180°-∠COD-∠D=180°-60°-30°=90°，
∴CD⊥OC，
∴CD是⊙O的切线．
证明：连接OC，∵∠CAB=∠D=30°，
∴∠COD=60°，
∴∠OCD=180°-∠COD-∠D=180°-60°-30°=90°，
∴CD⊥OC，
∴CD是⊙O的切线．
点评：本题考查的是切线的判定及圆周角定理、三角形内角和定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
如图，线段AB经过圆心O，交⊙O于点A，C，点D在⊙O上，连接AD，BD，∠A=∠B=30°，圆的半径R．
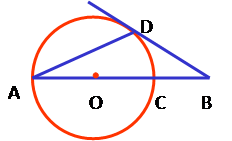
如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD=∠B=30°，边BD交圆于点D．
如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD=∠B=30°，边BD交圆于点D．