题目内容
在△ABC中,∠ACB=90°,AC=BC,点D为线段AC上的一点(不和点A、C重合),点E在线段BD的延长线,点F在线段BD上,连接CE、CF、AE,且∠ECF=90°,CE=CF,过点F作FG⊥BD分别交线段BC、线段AC的延长线于点P、G.
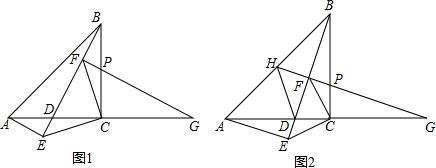
(1)如图l,求证:AC=CG;
(2)如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.

(1)如图l,求证:AC=CG;
(2)如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.
考点:全等三角形的判定与性质
专题:
分析:(1)证明∠FCG=∠ECB,∠DBC=∠DGF;进而证明△BCE≌△GCF,问题即可解决.
(2)首先证明△BCE≌△GCF,得到AD=BP;证明△AHD≌△BHP,问题即可解决.
(2)首先证明△BCE≌△GCF,得到AD=BP;证明△AHD≌△BHP,问题即可解决.
解答: 解:(1)证明:如图1
解:(1)证明:如图1
∵∠BCG=180°-∠ACB=90°=∠ECF
∴∠BCG+∠BCF=∠ECF+∠BCF,即∠FCG=∠ECB;
∵FG⊥BD,
∴∠DFG=90°,
∴∠DBC+∠BDG=90°,
又∵∠DGF+∠BDG=90°,
∴∠DBC=∠DGF;
在△BCE和△GCF中,
,
∴△BCE≌△GCF(AAS),
∴CB=CG,
又∵AC=CB,
∴AC=CG.
(2)如图2,证明:
在△BDC与△GPC中,
,
∴△BDC≌△GPC(ASA),
∴CD=CP,而AC=BC,
∴AD=BP;
∵AC=BC,
∴∠A=∠B;
在△AHD与△BHP中,
,
∴△AHD≌△BHP(SAS),
∴∠BHG=∠AHD.
 解:(1)证明:如图1
解:(1)证明:如图1∵∠BCG=180°-∠ACB=90°=∠ECF
∴∠BCG+∠BCF=∠ECF+∠BCF,即∠FCG=∠ECB;
∵FG⊥BD,
∴∠DFG=90°,
∴∠DBC+∠BDG=90°,
又∵∠DGF+∠BDG=90°,
∴∠DBC=∠DGF;
在△BCE和△GCF中,
|
∴△BCE≌△GCF(AAS),
∴CB=CG,
又∵AC=CB,
∴AC=CG.
(2)如图2,证明:
在△BDC与△GPC中,
|
∴△BDC≌△GPC(ASA),
∴CD=CP,而AC=BC,
∴AD=BP;
∵AC=BC,
∴∠A=∠B;
在△AHD与△BHP中,
|
∴△AHD≌△BHP(SAS),
∴∠BHG=∠AHD.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是深入分析、大胆猜测、合理推断、科学论证.

练习册系列答案
相关题目
⊙O的半径为4cm,点P和圆心的距离为8cm,则过P点的⊙O的两条切线的夹角是( )
| A、30° | B、60° |
| C、90° | D、120° |
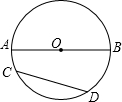 如图,AB是⊙O的直径,CD的是⊙O中非直径的任意一条弦,试比较AB与CD的大小,并说明理由.
如图,AB是⊙O的直径,CD的是⊙O中非直径的任意一条弦,试比较AB与CD的大小,并说明理由. 如图,已知AB=2的线段在线段MN上左右平移,MN=5,以A为中心顺时针旋转针M,以B为中心逆时针旋转点N,使M、N两点重合成一点,构成△ABC,设AM=x.
如图,已知AB=2的线段在线段MN上左右平移,MN=5,以A为中心顺时针旋转针M,以B为中心逆时针旋转点N,使M、N两点重合成一点,构成△ABC,设AM=x.