题目内容
1. 如图所示,在△ABC中,AB=AC,AD⊥BC于D,点E、F分别为边AD、CE的中点,且S阴影=4m2,则S△ABC=16m2.
如图所示,在△ABC中,AB=AC,AD⊥BC于D,点E、F分别为边AD、CE的中点,且S阴影=4m2,则S△ABC=16m2.
分析 如图,因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,△EBC与△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等积变换可解答.
解答 解:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF=$\frac{1}{2}$EC,高相等;
∴S△BEF=$\frac{1}{2}$S△BEC,
同理得,S△EBC=$\frac{1}{2}$S△ABC,
∴S△BEF=$\frac{1}{4}$S△ABC,且S阴影=4m2,
∴S△ABC=16m2.
故答案为:16.
点评 本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.

练习册系列答案
相关题目
13.气象台为了预报台风,首先要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
| A. | 西太平洋 | B. | 距电白500海里 | C. | 北纬28°,东经36° | D. | 湛江附近 |
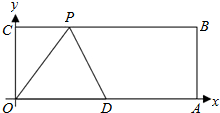 已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时.
已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时.