题目内容
【题目】我们把两边之比为整数的三角形称为倍比三角形.其中,这个整数比称为倍比,第三条边叫做该三角形的底.
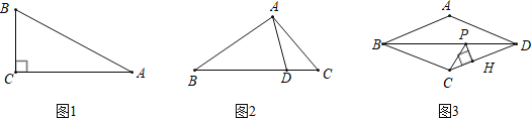
(1)如图1,△ABC是以AC为底的倍比三角形,倍比为3,若∠C=90°,AC=2![]() ,求BC的长;
,求BC的长;
(2)如图2,△ABC中,D为BC边上一点,BD=3,CD=1,连结AD.若AC=2,求证:△ABD是倍比三角形,并求出倍比;
(3)如图3,菱形ABCD中,∠BAD为钝角,P为对角线BD上一动点,过P作PH⊥CD于H、当CP+PH的值最小时,APCD恰好是以PD为底的倍比三角形,记倍比为x,![]() =y,求y关于x的函数关系式.
=y,求y关于x的函数关系式.
【答案】(1)1;(2)见解析,倍比为2;(3)y=![]()
【解析】
(1)由![]() 是以
是以![]() 为底的倍比三角形,倍比为
为底的倍比三角形,倍比为![]() ,推出
,推出![]() ,根据勾股定理构建方程即可解决问题.
,根据勾股定理构建方程即可解决问题.
(2)证明![]() ,可得
,可得![]() ,解决问题.
,解决问题.
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,此时
,此时![]() 的值最小.不妨设
的值最小.不妨设![]() ,由
,由![]() ,得到
,得到![]() ,证明
,证明![]() ,可得
,可得![]() ,即
,即![]() ,在
,在![]() 中,根据
中,根据![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(1)∵![]() 是以
是以![]() 为底的倍比三角形,倍比为
为底的倍比三角形,倍比为![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
(2)∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() 是倍比三角形,倍比为
是倍比三角形,倍比为![]()
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,此时
,此时![]() 的值最小
的值最小
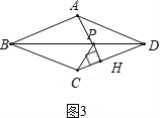
不妨设![]() ,由
,由![]() ,得到
,得到![]()
∵![]() 是以
是以![]() 为底的倍比三角形,倍比为
为底的倍比三角形,倍比为![]()
∴![]() ,即
,即![]()
∵四边形![]() 是菱形
是菱形
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]() ,即
,即![]()
在![]() 中,∵
中,∵![]()
∴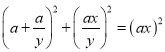
∴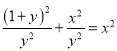
∴![]()
∴![]()

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目