题目内容
如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D处与C、B在同一直线上，已知AC=36米，CD=18米，求荷塘宽BD为多少米？（取| 3 |
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：直角三角形ABC中，利用边角关系求得BC的值，再根据荷塘宽BD=BC-CD，计算求得结果．
解答：解：由题意知：∠CAB=60°，△ABC是直角三角形，
在Rt△ABC中，tan60°=
，
即
=
，…（2分）
∴BC=36
，
∴BD=BC-CD=36
-18≈44．
答：荷塘宽BD约为44米．
解：由题意知：∠CAB=60°，△ABC是直角三角形，在Rt△ABC中，tan60°=
| BC |
| AC |
即
| BC |
| 36 |
| 3 |
∴BC=36
| 3 |
∴BD=BC-CD=36
| 3 |
答：荷塘宽BD约为44米．
点评：本题考查了解直角三角形的应用，解题的关键是利用俯角的定义将题目中的相关量转化为直角三角形ABC中的有关元素．
练习册系列答案
相关题目
工地上有甲、乙二块铁板，铁板甲形状为等腰三角形，其顶角为45°，腰长为12cm；铁板乙形状为直角梯形，两底边长分别为4cm、10cm，且有一内角为60°．现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是（ ）
| A、甲板能穿过，乙板不能穿过 |
| B、甲板不能穿过，乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
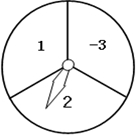如图转盘，分成三个相同的扇形，3个扇形分别标有数字1、2、-3，指针位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置，并相应得到一个数（指针指向两个扇形的交线时，重新转动转盘）．