题目内容
7. 如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)
如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)
分析 作BF⊥AD于F,设BC=x米,根据正弦的定义求出CE,根据余弦的定义求出BE,用x表示出DE,根据等腰直角三角形的性质求出AD,表示出AF,根据正切的概念列出方程,解方程即可.
解答 解: 作BF⊥AD于F,
作BF⊥AD于F,
设BC=x米,
∵∠CBE=60°,
∴BE=BC×cos∠CBE=$\frac{1}{2}$x,CE=BC×sin∠CBE=$\frac{\sqrt{3}}{2}$x,
∵CD=200米,
∴DE=200-$\frac{\sqrt{3}}{2}$x,
则BF=DE=200-$\frac{\sqrt{3}}{2}$x,
∵∠CAD=45°,
∴AD=CD=200,
则AF=200-$\frac{1}{2}$x,
∵tan∠BAF=$\frac{BF}{AF}$,
∴$\frac{200-\frac{\sqrt{3}}{2}x}{200-\frac{1}{2}x}$=$\frac{\sqrt{3}}{3}$,
解得,x=200($\sqrt{3}$-1)≈146米.
答:电缆BC至少146米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 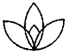 | B. |  | C. | 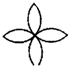 | D. | 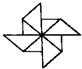 |
15.下列实数中$\sqrt{7}$,-(-π),|-3|,3中,最大的是( )
| A. | $\sqrt{7}$ | B. | -(-π) | C. | |-3| | D. | 3 |
2.在下列调查中,适宜采用普查方式的是( )
| A. | 了解全国中学生的视力情况 | |
| B. | 了解九(1)班学生鞋子的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查郑州电视台《郑州大民生》栏目的收视率 |
12. 已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 112° | B. | 114° | C. | 116° | D. | 118° |
19.在平面直角坐标系中,如果抛物线y=3x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系中抛物线的解析式是( )
| A. | y=3(x-2)2+2 | B. | y=3(x+2)2-2 | C. | y=3(x-2)2+2 | D. | y=3(x+2)2+2 |
16.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
| A. | $\frac{25}{2}$mm | B. | $\frac{25}{2}$$\sqrt{3}$mm | C. | $\frac{25}{4}$mm | D. | $\frac{25}{4}$$\sqrt{3}$mm |
