题目内容
(1)化简:3
-9(
-
);
(2)解方程:(x-3)2=(2x-1)(x-3).
| 3 |
| 8 |
|
(2)解方程:(x-3)2=(2x-1)(x-3).
考点:二次根式的加减法,解一元二次方程-因式分解法
专题:
分析:(1)先把各根式化为最简二次根式,再合并同类项即可;
(2)先移项,再提取公因式,求出x的值即可.
(2)先移项,再提取公因式,求出x的值即可.
解答:解:(1)原式=3
-9
+9
=3
-18
+3
=6
-18
;
(2)移项得,(x-3)2-(2x-1)(x-3)=0,
提取公因式得,(3-x)(x+2)=0,解得x1=3,x2=-2.
| 3 |
| 8 |
|
=3
| 3 |
| 2 |
| 3 |
=6
| 3 |
| 2 |
(2)移项得,(x-3)2-(2x-1)(x-3)=0,
提取公因式得,(3-x)(x+2)=0,解得x1=3,x2=-2.
点评:本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
若|a|=1,b2=4,且ab<0,则a-b的值是( )
| A、-3或3 | B、-1或3 |
| C、3 | D、-3 |
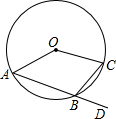 如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=
如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=
 如图,已知△ABC(AC<BC),用尺规作图,在BC上作出一点P,使PA+PC=BC,并简述理由或依据(不写作法,保留作图痕迹).
如图,已知△ABC(AC<BC),用尺规作图,在BC上作出一点P,使PA+PC=BC,并简述理由或依据(不写作法,保留作图痕迹).