题目内容
 如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形.
(2)若AD=4,CD=3,求四边形OCED的面积.
考点:菱形的判定与性质
专题:
分析:(1)根据矩形的性质得出AC=2CO,BD=2DO,AC=BD,推出DO=CO,先求出四边形OCED是平行四边形,再根据菱形的判定求出即可;
(2)根据矩形的性质得出AO=CO,∠ADC=90°,求出△ADC的面积为6,即可求出S△ADO=S△DCO=
S△ADC=3,证△DCE≌△COD,得出S△DCE=S△COD=3,即可求出四边形OCED的面积.
(2)根据矩形的性质得出AO=CO,∠ADC=90°,求出△ADC的面积为6,即可求出S△ADO=S△DCO=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是矩形,
∴AC=2CO,BD=2DO,AC=BD,
∴DO=CO,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED是菱形;
(2)解:∵四边形ABCD是矩形,
∵AO=CO,∠ADC=90°,
∵AD=4,DC=3,
∴△ADC的面积为
×AD×DC=6,
∴S△ADO=S△DCO=
S△ADC=3,
∵四边形OCED是菱形,
∴DE=CO,DO=CE,
在△DCE和△COD中,
,
∴△DCE≌△COD(SSS),
∴S△DCE=S△COD=3,
∴四边形OCED的面积是3+3=6.
∴AC=2CO,BD=2DO,AC=BD,
∴DO=CO,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED是菱形;
(2)解:∵四边形ABCD是矩形,
∵AO=CO,∠ADC=90°,
∵AD=4,DC=3,
∴△ADC的面积为
| 1 |
| 2 |
∴S△ADO=S△DCO=
| 1 |
| 2 |
∵四边形OCED是菱形,
∴DE=CO,DO=CE,
在△DCE和△COD中,
|
∴△DCE≌△COD(SSS),
∴S△DCE=S△COD=3,
∴四边形OCED的面积是3+3=6.
点评:本题考查了矩形的性质,菱形的判定,平行四边形的判定和性质,三角形的面积的应用,能求出四边形OCED是菱形和各个三角形的面积是解此题的关键,难度适中.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图所示的图形经过折叠可以得到一个正方体,则该正方体中,与“我”字一面相对的面上的字是( )
如图所示的图形经过折叠可以得到一个正方体,则该正方体中,与“我”字一面相对的面上的字是( )| A、你 | B、武 | C、候 | D、梦 |
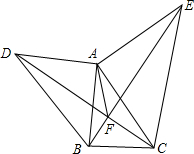 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点. 平行四边形ABCD,过C任意作一条直线交AB于E,BF⊥CE于点F,DG⊥CE于点G,AH⊥DG于点H,从图形中找出(不是平行四边形的一组对边的)两条相等的线段,并证明.
平行四边形ABCD,过C任意作一条直线交AB于E,BF⊥CE于点F,DG⊥CE于点G,AH⊥DG于点H,从图形中找出(不是平行四边形的一组对边的)两条相等的线段,并证明. 在菱形ABCD中,∠BAF=∠DAE,求证:BD∥EF.
在菱形ABCD中,∠BAF=∠DAE,求证:BD∥EF.