题目内容
 如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M,试说明M为AB的中点.
如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M,试说明M为AB的中点.考点:菱形的性质
专题:证明题
分析:如图,连接BD,由菱形的对角线互相垂直和平行线的判定得到:ME∥BD,则ME是△ABD的中位线,故M为AB的中点.
解答: 解:如图,连接BD.
解:如图,连接BD.
∵四边形ABCD是菱形,
∴AC⊥BD.
又∵EF⊥AC,
∴EF∥BD.
又∵点E是AD边的中点,
∴ME是△ABD的中位线,
∴M为AB的中点.
 解:如图,连接BD.
解:如图,连接BD.∵四边形ABCD是菱形,
∴AC⊥BD.
又∵EF⊥AC,
∴EF∥BD.
又∵点E是AD边的中点,
∴ME是△ABD的中位线,
∴M为AB的中点.
点评:本题考查了菱形的性质.解题时利用了菱形的对角线互相垂直和三角形的中位线定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,△A′B′C′与△ABC成轴对称的是( )
A、 |
B、 |
C、 |
D、 |
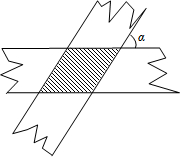 如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )
如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|
 如图所示的图形经过折叠可以得到一个正方体,则该正方体中,与“我”字一面相对的面上的字是( )
如图所示的图形经过折叠可以得到一个正方体,则该正方体中,与“我”字一面相对的面上的字是( )| A、你 | B、武 | C、候 | D、梦 |
(x2+ax+8)(x2-3x+b)展开式中不含x3和x2项,则a、b的值分别为( )
| A、a=3,b=1 |
| B、a=-3,b=1 |
| C、a=0,b=0 |
| D、a=3,b=8 |
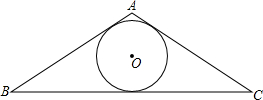 如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.
如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.