题目内容
如果x2-4x+1=0,那么
= .
| x4-4x2+1 |
| x2 |
考点:分式的化简求值
专题:
分析:完全平方公式:(a±b)2=a2±2ab+b2,先把x2-4x+1=0两边同除x(由题意可知x≠0),得到x+
=4,然后把该式子两边平方即可得出x2+
的值,再把原式化简.把x2+
的值代入进行计算即可.
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
解答:解:∵x2-4x+1=0,
∴x-4+
=0,
即x+
=4,
∴x2+
=(x+
)2-2,
=42-2,
=14,
原式=x2-4+
=14-4
=10.
故答案为:10.
∴x-4+
| 1 |
| x |
即x+
| 1 |
| x |
∴x2+
| 1 |
| x2 |
| 1 |
| x |
=42-2,
=14,
原式=x2-4+
| 1 |
| x2 |
=14-4
=10.
故答案为:10.
点评:本题考查的是分式的化简求值,解题关键是利用隐含条件x≠0,x2-4x+1=0两边同除x得到x+
=4,利用x和
互为倒数乘积是1与完全平方公式来进行解题.
| 1 |
| x |
| 1 |
| x |

练习册系列答案
相关题目
若
=
,则
=( )
| a |
| b |
| 2 |
| 9 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、-
|
若2x-y-2013=0,则2y-4x+2014的值为( )
| A、2012 | B、-2012 |
| C、1 | D、-1 |
 如图,已知△ABC的面积等于20cm2,周长等于10cm,△ABC两条内角平分线相交于点O,则点O到BC边的距离为
如图,已知△ABC的面积等于20cm2,周长等于10cm,△ABC两条内角平分线相交于点O,则点O到BC边的距离为 画出下面物体的正投影(正三棱柱)
画出下面物体的正投影(正三棱柱)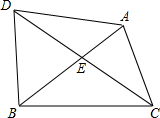 四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD=
四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD=