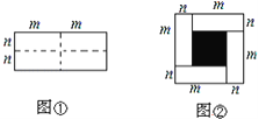
��Ŀ����
����Ŀ��������С����Ƶġ���![]() ��
��![]() ���ϵĸ��ߡ��ij߹���ͼ����.
���ϵĸ��ߡ��ij߹���ͼ����.
��֪��![]() .
.
������![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() .
.
��������ͼ��
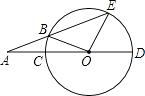
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶�������Ե�
�ij�Ϊ�뾶�������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() �·����ڵ�
�·����ڵ�![]() ��
��
������![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
�����߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤��.
֤�������� ![]() ����
���� ![]() ��
��
���![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() �Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
�Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
��![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() .
.
���߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
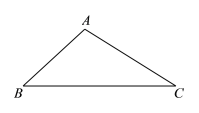
���𰸡���1������������2��������
��������
��1�����ü������Ի�����Ӧ�ļ���ͼ�Σ�
��2��ͨ����ͼ�õ�AM=AN��MP=NP��������߶δ�ֱƽ���ߵ����ʶ������涨�����ж�AP���߶�MN�Ĵ�ֱƽ���ߣ��Ӷ��õ�AD��BC��
��1����ȷ��ȫͼ�Σ�
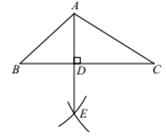
��2��֤������AM=AN��MP=NP��
��AP���߶�MN�Ĵ�ֱƽ���ߣ���һ���߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�
��AD��BC��D�����߶�ADΪ��ABC�ı�BC�ϵĸߣ�
�ʴ�ΪAN��NP����һ���߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�

��ϰ��ϵ�д�
�����Ŀ