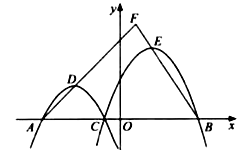
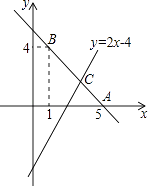��Ŀ����
����Ŀ������![]() ��
��![]() �������϶�Ӧ����Ϊ
�������϶�Ӧ����Ϊ![]() ��
��![]() �����
�����![]() ��
��![]() ��
��![]() ֮��ľ��룬����
֮��ľ��룬����![]() .��֪����������
.��֪����������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ
��Ӧ�����ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ����
����![]() Ϊ������һ���㣬���Ӧ����Ϊ
Ϊ������һ���㣬���Ӧ����Ϊ![]() .
.
��1������![]() ����
����![]() ��
��![]() �ľ�����ȣ����
�ľ�����ȣ����![]() ��Ӧ������_________.
��Ӧ������_________.
��2���������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ������
�������ڣ������![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3������![]() ��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����
��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����![]() ��ÿ��3����λ���������˶�����
��ÿ��3����λ���������˶�����![]() ��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��
��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��![]() ����
����![]() ��
��![]() �ľ�����ȣ�
�ľ�����ȣ�
���𰸡���1��1����2��-3��5����3��![]() ��
��![]()
��������
��1���ȸ��ݷǸ��Եõ�a,b��ֵ���ٸ����е�����ʼ�����⣻
��2������������������������⣻
��3����������ֵ���![]() δ�ϵ�
δ�ϵ�![]() ʱ�͵���
ʱ�͵���![]() �ϵ�
�ϵ�![]() ��
��![]() ��
��![]() �غ�ʱ���ֱ������⼴��.
�غ�ʱ���ֱ������⼴��.
��1����![]()
��a=-2��b=4
������������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ-2��4��
��Ӧ�����ֱ�Ϊ-2��4��
�ߵ�![]() ����
����![]() ��
��![]() �ľ������
�ľ������
��P���ʾ����Ϊ![]()
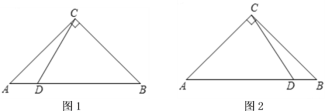
���1��
��2�����������
������![]() �ڵ�
�ڵ�![]() �����ʱ
�����ʱ
![]()
��ã�![]()
������![]() �ڵ�
�ڵ�![]() ���Ҳ�ʱ
���Ҳ�ʱ
![]()
��ã�![]()
��3����![]() ����
����![]() ����
����![]() ��
��![]() �ľ������
�ľ������
��![]() ���
���![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
������![]() δ�ϵ�
δ�ϵ�![]() ʱ
ʱ
![]()
��ã�![]()
������![]() �ϵ�
�ϵ�![]() ��
��![]() ��
��![]() �غ�ʱ
�غ�ʱ
![]()
��ã�![]()