题目内容
若x1=
-2是二次方程x2+ax+1=0的一个根,则a= ,该方程的另一个根x2= .
| 3 |
考点:一元二次方程的解,根与系数的关系
专题:
分析:根据根与系数的关系,根据两根之积,即可得到方程的另一根,再由两根之和即可得出一个关于a的方程,从而求得a的值.
解答:解:设方程的另一个根为x2,
∵x1=
-2是二次方程x2+ax+1=0的一个根,
∴x1•x2=1,即(
-2)x2=1,
∴x2=-
-2,
∴x1+x2=-a,即
-2-
-2=-a,解得a=4,
故答案为4,-
-2.
∵x1=
| 3 |
∴x1•x2=1,即(
| 3 |
∴x2=-
| 3 |
∴x1+x2=-a,即
| 3 |
| 3 |
故答案为4,-
| 3 |
点评:本题考查了一元二次方程解的定义和根与系数的关系,注意在解题时要重视解题思路的逆向分析.

练习册系列答案
相关题目
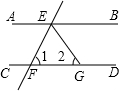 如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?
如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?