题目内容
8. 如图,在平面直角坐标系中,△AOB是边长为2的等边三角形,直线L交x轴于点C(2,0),交边AB于E,且△ADE与△COD的面积相等,点E在双曲线y=$\frac{k}{x}$(x<0)上,则k=-$\frac{3\sqrt{3}}{4}$.
如图,在平面直角坐标系中,△AOB是边长为2的等边三角形,直线L交x轴于点C(2,0),交边AB于E,且△ADE与△COD的面积相等,点E在双曲线y=$\frac{k}{x}$(x<0)上,则k=-$\frac{3\sqrt{3}}{4}$.
分析 连接AC,先由等边三角形及等腰三角形的性质判断出△ABC是直角三角形,再由S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,可得出S△AEC=S△AOC,故可得出AE的长,再由中点坐标公式求出E点坐标,把点E代入反比例函数y=$\frac{k}{x}$即可求出k的值.
解答  解:连接AC,
解:连接AC,
∵△AOB是边长为2的等边三角形,
∴点B的坐标为(-2,0),OA=2,
∵C(2,0),
∵AO=OC=2,
∴∠OCA=∠OAC,
∵∠AOB=60°,
∴∠ACO=30°,∠B=60°,
∴∠BAC=90°,
∴点A的坐标为(-1,$\sqrt{3}$),
∵S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,
∴S△AEC=S△AOC=$\frac{1}{2}$×AE•AC=$\frac{1}{2}$×CO×$\sqrt{3}$,
即$\frac{1}{2}$AE•2$\sqrt{3}$=$\frac{1}{2}$×2×$\sqrt{3}$,
∴AE=1.
∴E点为AB的中点(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)
把E点(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)代入y=$\frac{k}{x}$得,k=(-$\frac{3}{2}$)×$\frac{\sqrt{3}}{2}$=-$\frac{3\sqrt{3}}{4}$.
故答案为:-$\frac{3\sqrt{3}}{4}$.
点评 本题考查的是反比例函数综合题,涉及到直角三角形的判定与性质、等边三角形的性质、三角形的面积等有关知识,综合性较强.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18.点(-2016,2016)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.到了劳动课时,刚好是小明和小聪两位同学值日,教室里有两样劳动工具:扫把和拖把,小明与小聪用“剪刀,石头,布”的游戏方法决定谁胜了就让谁使用扫把,则小明出“剪刀”后,能胜出的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
 点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.
点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点. 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.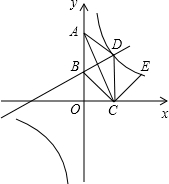 如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.
如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.