题目内容
16．
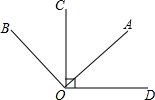如图，OA⊥OB，OC⊥OD，∠AOC=α，则∠BOD=（ ）| A． | 180°-2α | B． | 2α-90° | C． | 90°+$\frac{1}{2}$α | D． | 180°-α |
分析 根据垂直的定义可得∠AOC+∠AOD=90°，然后求出∠AOD+∠BOD=180°，从而得解．
解答 解：∵OA⊥OB，OC⊥OD，
∴∠AOC+∠AOD=90°，∠AOD+∠BOC=90°，
∴∠BOC=∠BOD，
∴∠BOD=90°+∠BOC=90°+（90°-∠AOD）．
∴∠BOD=180°-α，
故选D．
点评 本题考查了垂线的定义，是基础题，熟记概念是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
6．下列等式中正确的是（ ）
| A． | a3•（-3a2）=-3a6 | B． | 6（b-a）2-2（a-b）=2（a-b）（3a-3b-1） | ||
| C． | （-2a-3b）（2a-3b）=4a2-9b2 | D． | （-a）6÷（-a）3=a2 |
7．广东某县生产柚子，其中A村有柚子200吨，B村有柚子280吨，先将这些柚子运到C、D两个仓库．已知C仓库可存储260吨，D仓库可存储220吨，从A村运往C、D两处的费用分别为每吨20元和25元；从B村运往C、D两仓库的费用分别为每吨16元和20元．设从A村运往C仓库的柚子重量为x吨，A、B两村运往两仓库的柚子运输费用分别为yA元，yB元．
（1）请填写下表，并求出yA，yB与x之间的函数关系式．
（2）考虑到B村的经济承受能力，B村的柚子运费不得超过4800元，在这种情况下，请问怎样调运，才能使两村运费之和最小？最小是多少？求出这个最小值．
（1）请填写下表，并求出yA，yB与x之间的函数关系式．
| C | D | 总计 | |
| A | x吨 | 200-x | 200吨 |
| B | 260-x | x+20 | 280吨 |
| 总计 | 260吨 | 220吨 | 480吨 |
11．若关于x的不等式mx-n＞0的解集是x＜$\frac{1}{4}$，则关于x的不等式（n-m）x＞（m+n）的解集是（ ）
| A． | x＜-$\frac{5}{3}$ | B． | x＞-$\frac{5}{3}$ | C． | x＜$\frac{5}{3}$ | D． | x＞$\frac{5}{3}$ |
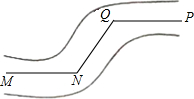如图，一条公路两次转弯后又回到原来的方向，如果第一次转弯时∠N=120°，则第二次转弯时∠Q=120°．