题目内容
如图,圆O的半径为r.
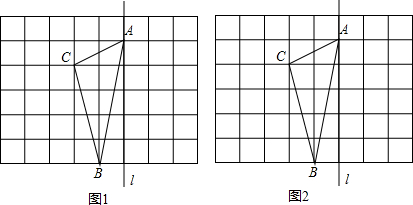
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为 .
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.

(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.

考点:正多边形和圆
专题:
分析:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出;
(2)根据对角线相等且互相平分的四边形是矩形,顺次连接矩形的四个顶点即可作出;
(3)连接AC,利用相似三角形的性质求得DG的长,则BC和EF即可利用x和r表示出来,从而得到L关于x的函数关系式,利用二次函数的性质求解.
(2)根据对角线相等且互相平分的四边形是矩形,顺次连接矩形的四个顶点即可作出;
(3)连接AC,利用相似三角形的性质求得DG的长,则BC和EF即可利用x和r表示出来,从而得到L关于x的函数关系式,利用二次函数的性质求解.
解答: 解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
△ABC就是所求的三角形;
(2)在直角△ABD中,AD=
=
,
则BC=AD=
,CD=AB=x.
则矩形的周长是:2x+2
,
故答案是:2x+2
;
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG•AD,
∴DG=
=
,
∴BC=EF=AD-2DG=2r-
.
则L=4x+4r-
.
当x=-
=r时,L取得最大值.最大值是:6r.
 解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.△ABC就是所求的三角形;
(2)在直角△ABD中,AD=
| AC2-AB2 |
| 4r2-x2 |
则BC=AD=
| 4r2-x2 |
则矩形的周长是:2x+2
| 4r2-x2 |
故答案是:2x+2
| 4r2-x2 |
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG•AD,
∴DG=
| CD2 |
| AD |
| x2 |
| 2r |
∴BC=EF=AD-2DG=2r-
| x2 |
| r |
则L=4x+4r-
| 2x2 |
| r |
当x=-
| 4 | ||
-
|
点评:此题考查了正多边形和圆的知识.题目难度不大,利用x和半径r表示出BD和EF的长度是关键.

练习册系列答案
相关题目
地球七大洲的总面积约是149 480 000km2,对这一数据精确到10000000可表示为( )
| A、149km2 |
| B、1.5×108km2 |
| C、1.49×108km2 |
| D、1.50×108km2 |
若一元二次方程x2-4x-5=0的根是直角三角形斜边上的中线长,则这个直角三角形的斜边长为( )
| A、2 | B、10 | C、2或10 | D、5 |
 已知△ABC中,AB=AC,CD⊥AB于D.
已知△ABC中,AB=AC,CD⊥AB于D. 一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )