题目内容
7.有四个三角形,分别满足下列条件:(1)一个内角等于另外两个内角之和;
(2)三个内角之比为3:4:5;
(3)三边之比为5:12:13;
(4)三边长分别为7、24、25.
其中直角三角形有3个.
分析 (1)(2)根据三角形的内角和等于180°,求出三角形中最大的角的度数,然后即可判断;
(3)(4)根据勾股定理逆定理列式进行计算即可得解.
解答 解:(1)∵一个角等于另外两个内角之和,
∴这个角=$\frac{1}{2}$×180°=90°,是直角三角形;
(2)三个内角之比为3:4:5,
∴最大的角=$\frac{5}{3+4+5}$×180°=$\frac{5}{12}$×180°<90°,是锐角三角形;
(3)设三边分别为5k,12k,13k,
则(5k)2+(12k)2=25k2+144k2=169k2=(13k)2,是直角三角形;
(4)∵72+242=49+576=625=252,
∴三边长分别为7,24,25的三角形是直角三角形.
综上所述,是直角三角形的有(1)(3)(4)共3个.
故答案为3.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.也考查了三角形内角和定理以及直角三角形的定义.

练习册系列答案
相关题目
2.若点B在直线AC上,AB=10,BC=5,则A、C两点间的距离是( )
| A. | 5 | B. | 15 | C. | 5或15 | D. | 不能确定 |
16.下列说法正确的是( )
| A. | +a是正数 | B. | -a是负数 | ||
| C. | a与-a互为相反数 | D. | a与-a一定有一个是负数 |
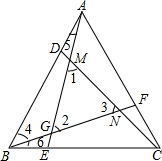 如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.
如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.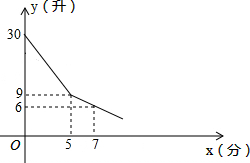 某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.
某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.