题目内容
19．一个正多边形的一个内角等于它的一个外角的2倍，这个正多边形是几边形？这个正多边形的内角和是多少？分析 设这个正多边的外角为x°，则内角为2x°，根据内角和外角互补可得x+2x=180，解可得x的值，再利用外角和360°÷外角度数可得边数，利用内角和定理求得答案即可．
解答 解：设这个正多边的外角为x°，由题意得：
x+2x=180，
解得：x=60，
360°÷60°=6．
所以这个正多边形为6边形；
内角和为（6-2）×180°=720°．
点评 此题主要考查了多边形的内角和外角，关键是计算出外角的度数，进而得到边数．
练习册系列答案
相关题目
7．将抛物线y=（x-1）2+2沿x轴折叠后得到的新抛物线的解析式为（ ）
| A． | y=（x+1）2-2 | B． | y=（x-1）2-2 | C． | y=-（x-1）2+2 | D． | y=（x+1）2+2 |
图中所有的边形均是正方形，所有三角形都是直角三角形，最大正方形的边长为2cm，则正方形A、B、C、D的面积和是4cm2．
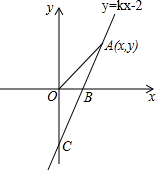如图，直线y=kx-2与x轴，y轴分别交于B，C两点，其中OB=1．