题目内容
13. 如图AD,AE分别是△ABC的角平分线和高,且∠B=40°,∠C=68°,求∠ADE度数.
如图AD,AE分别是△ABC的角平分线和高,且∠B=40°,∠C=68°,求∠ADE度数.
分析 根据垂直得出∠AEB=∠AEC=90°,根据三角形内角和定理求出∠BAC,根据角平分线定义求出∠DAC,求出∠CAE,解答即可.
解答 解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∵∠B=40°,∠C=68°,
∴∠EAC=90°-∠C=22°,∠BAC=180°-40°-68°=72°,
∵AD平分∠BAC,
∴∠CAD=36°,
∵∠EAC=22°,
∴∠DAE=36°-22°=14°,
∵∠AED=90°,
∴∠ADE=90°-∠DAE=76°
点评 本题考查了三角形内角和定理,垂直定义,角平分线定义的应用,能运用定理求出各个角的度数是解此题的关键,注意:三角形的内角和等于180°.

练习册系列答案
相关题目
3.下列各组数中,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 3k,4k,5k(k>0) | C. | 6,8,11 | D. | 5,12,23 |
8.在下面图形:线段、等腰三角形、正方形、平行四边形、梯形中是中心对称图形的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
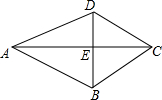 如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.
如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.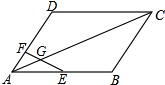 如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.
如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.