题目内容
若a、b、c均为整数，且|a-b|3+|c-a|2=1，求|a-c|+|c-b|+|b-a|的值．
考点：绝对值
专题：
分析：先判断出a、b、c有两个数相等，不妨设为a=b，然后表示出c，再求出|a-c|，即可得解．
解答：解：∵a，b，c均为整数，且|a-b|3+|c-a|2=1，
∴a、b、c有两个数相等，
不妨设为a=b，
则|c-a|=1，
∴c=a+1或c=a-1，
∴|a-c|=|a-a-1|=1或|a-c|=|a-a+1|=1，
∴|a-c|+|c-b|+|b-a|=1+1=2．
∴a、b、c有两个数相等，
不妨设为a=b，
则|c-a|=1，
∴c=a+1或c=a-1，
∴|a-c|=|a-a-1|=1或|a-c|=|a-a+1|=1，
∴|a-c|+|c-b|+|b-a|=1+1=2．
点评：本题考查了绝对值的性质和有理数的乘方，判断出a、b、c有两个数相等是解题的关键．
练习册系列答案
相关题目
代数式xy2-y2（ ）
| A、它是单项式 |
| B、它是x，y的积的平方与y平方的差 |
| C、它是三次二项式 |
| D、它的二次项系数为1 |
如图：Rt△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从A点开始沿AB边向点B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．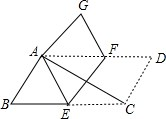
将?ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处（如图）． 
如图，矩形ABCD中，AB=6，BC=8，E是BC边上的一定点，P是CD边上的一动点（不与点C、D重合），M，N分别是AE、PE的中点，记MN的长度为a，在点P运动过程中，a不断变化，则a的取值范围是
