题目内容
13.先阅读,后解答:$\frac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=$\frac{3+\sqrt{6}}{3-2}$=3+$\sqrt{6}$
像上述解题过程中,$\sqrt{3}$-$\sqrt{2}$与$\sqrt{3}$+$\sqrt{2}$相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)$\sqrt{3}$的有理化因式是$\sqrt{3}$; $\sqrt{5}$+2的有理化因式是$\sqrt{5}$-2.
(2)将下列式子进行分母有理化:
$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;$\frac{1}{3+\sqrt{6}}$=1-$\frac{\sqrt{6}}{3}$.
(3)已知a=$\frac{1}{2+\sqrt{3}}$,b=2-$\sqrt{3}$,比较a与b的大小关系.
分析 (1)根据题意找出各式的有理化因式即可;
(2)各式分母有理化即可;
(3)把a分母有理化,比较即可.
解答 解:(1)$\sqrt{3}$的有理化因式是$\sqrt{3}$,$\sqrt{5}$+2的有理化因式是$\sqrt{5}$-2;
故答案为:$\sqrt{3}$;$\sqrt{5}$-2;
(2)原式=$\frac{2\sqrt{5}}{5}$;原式=$\frac{3-\sqrt{6}}{3}$=1-$\frac{\sqrt{6}}{3}$;
故答案为:$\frac{2\sqrt{5}}{5}$;1-$\frac{\sqrt{6}}{3}$;
(3)a=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$=b.
点评 此题考查了分母有理化,以及实数大小比较,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
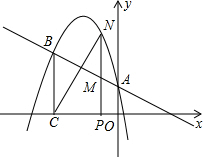 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).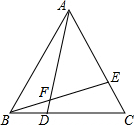 如图,D、E分别为等边△ABC的边BC、AC上的点,且BD=CE,连结BE、AD交于F,求证:∠AFE=60°.
如图,D、E分别为等边△ABC的边BC、AC上的点,且BD=CE,连结BE、AD交于F,求证:∠AFE=60°.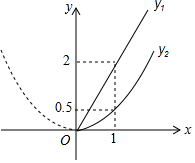 随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)
随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)