题目内容
12.图1,图2是两张形状、大小完全相同的6×6方格纸,方格纸中的每个小正方形的边长均为1,所求作的图形各顶点也在格点上,(1)在图1中画一个以点A,B为顶点的菱形(不是正方形),并求菱形周长;
(2)在图2中画一个以点A为所画的平行四边形对角线交点,且面积为6,求此平行四边形周长.
周长4$\sqrt{10}$ 周长6+2$\sqrt{5}$.
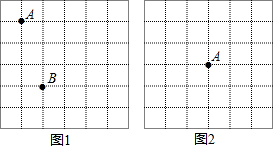
分析 (1)以AB为一边,根据菱形的四条边相等进行作图即可,根据AB的长,即可得到菱形的周长;
(2)以点A为所画的平行四边形对角线交点,根据平行四边形的面积为6进行作图即可,根据平行四边形的各边长即可得出其周长.
解答 解:(1)如图所示,菱形ABCD即为所求;
∵AB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴菱形ABCD的周长=4$\sqrt{10}$;
(2)如图所示,平行四边形BCDE即为所求;
∵BC=3,CD=$\sqrt{5}$,
∴平行四边形BCDE的周长=2(3+$\sqrt{5}$)=6+2$\sqrt{5}$.
点评 本题主要考查了菱形的性质以及平行四边形的性质,解题时首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
14.计算|-4+1|的结果是( )
| A. | -5 | B. | -3 | C. | 3 | D. | 5 |
7.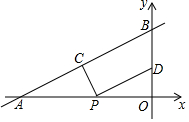 如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )
如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )
 如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )
如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )| A. | 3 | B. | 6 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
17.计算5-2正确的是( )
| A. | -10 | B. | $-\frac{1}{25}$ | C. | $\frac{1}{25}$ | D. | 25 |
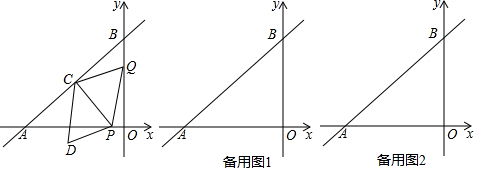
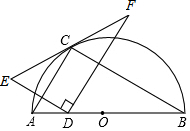 如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.
如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.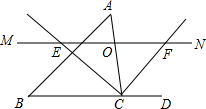 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.