题目内容
13.解方程组:$\left\{\begin{array}{l}{53x+47y=112}\\{47x+53y=88}\end{array}\right.$.分析 ①+②得到x与y的关系,用x表示y代入①求出x的值,把x的值代入③求出y的值,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{53x+47y=112①}\\{47x+53y=88②}\end{array}\right.$,
①+②得,x+y=2,
即y=2-x③,
把③代入①得,x=3,
把x=3代入③得,y=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解法,灵活运用代入法是解题的关键,注意整体思想在解题中的作用.

练习册系列答案
相关题目

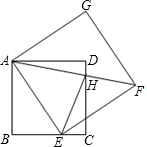 如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.
如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.