题目内容
 如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
①求证:EC⊥CD;
②当EO:OC=1:3,CD=4时,求⊙O的半径.
①证明:E为弦AB(非直径)的中点,O为圆心,
∴∠OEB=90°,
∵∠ECD=∠OEB=90°,
即EC⊥CD;
②解:∵CD∥AB,EO:OC=1:3,
∴ ,
,
设OC=BO=x,则OD=3x,又CD=4,
在Rt△OCD中,由OC2+CD2=OD2,x2+42=(3x)2,
解得:x1= ,x2=-
,x2=- (舍去),
(舍去),
∴BO= ,
,
即⊙O的半径为 .
.
分析:①根据垂径定理不难得出OE⊥AB.又有AB∥CM,由此便可证得;
②AB∥CD,不难得出EO:OC=1:3;然后用半径分别表示出OC,OD,CD,根据勾股定理来求出半径的值.
点评:本题主要考查了在圆内对垂径定理和勾股定理的综合运用.
∴∠OEB=90°,
∵∠ECD=∠OEB=90°,
即EC⊥CD;
②解:∵CD∥AB,EO:OC=1:3,
∴
 ,
,设OC=BO=x,则OD=3x,又CD=4,
在Rt△OCD中,由OC2+CD2=OD2,x2+42=(3x)2,
解得:x1=
 ,x2=-
,x2=- (舍去),
(舍去),∴BO=
 ,
,即⊙O的半径为
 .
.分析:①根据垂径定理不难得出OE⊥AB.又有AB∥CM,由此便可证得;
②AB∥CD,不难得出EO:OC=1:3;然后用半径分别表示出OC,OD,CD,根据勾股定理来求出半径的值.
点评:本题主要考查了在圆内对垂径定理和勾股定理的综合运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
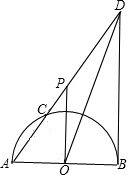 如图,已知:AB为⊙O的直径,AB=6
如图,已知:AB为⊙O的直径,AB=6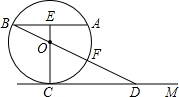 如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D. 如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°.
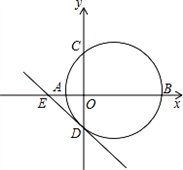
如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°. 如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(-
如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(- ,0).
,0).