Question

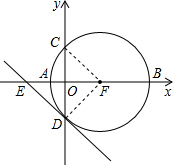
如图，已知以AB为直径的圆与x轴交于A、B两点，与y轴交于C、D两点，A、C 两点的坐标分别为A（-1，0）、C（0，3），直线DE交x轴交于点E（-

9

4

，0）．
（1）求该圆的圆心坐标和直线DE的解析式；
（2）判断直线DE与圆的位置关系，并说明理由．

Answer 1

分析：（1）设圆心为F，圆是半径为r，连接CF，根据点A、C的坐标表示出OC、OF的长度，然后利用勾股定理列式进行计算即可求出r的值，从而得到圆心的坐标，利用待定系数法列式进行计算即可求出直线DE的解析式；
（2）根据圆的对称性可得点D的坐标，连接DF，然后求出△DOE与△FOD相似，再根据相似三角形对应角相等求出∠ODE=∠OFD，从而推出∠EDF=90°，根据直线与圆的位置关系即可判断．

解答：解：（1）如图，设圆心为F，圆的半径为r，连接CF，
∵A（-1，0）、C（0，3），
∴OC=3，OF=r-1，
根据勾股定理，CF²=OC²+OF²，
即r²=3²+（r-1）²，
解得r=5，
r-1=4，
∴圆心坐标为（4，0），
根据圆的对称性，点D的坐标为（0，-3），
设直线DE的解析式为y=kx+b，
则

b=-3 - 9 4 k+b=0

，
解得

k=- 4 3 b=-3

，
∴直线DE的解析式为y=-

4

3

x-3；

（2）直线DE与圆相切．理由如下：
如图，连接DF，
则OE=

9

4

，OF=4，OD=3，

OE

OD

=

9 4

3

=

3

4

，

OD

OF

=

3

4

，
∴

OE

OD

=

OD

OF

，
又∵∠DOF，
∴△DOE∽△FOD，
∴∠ODE=∠OFD，
∵∠OFD+∠ODF=90°，
∴∠ODE+∠ODF=90°，
即∠EDF=90°，
∴FD⊥ED，
又∵点D在圆上，
∴直线DE与圆相切．

点评：本题是对一次函数的综合考查，主要有勾股定理，待定系数法求直线解析式，直线与圆相切的判定，作出辅助线构造出直角三角形是解题的关键．