题目内容
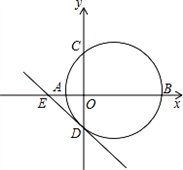
如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(﹣1,0)、C(0,3),直线DE交x轴交于点E(﹣ ,0).
,0).
(1)求该圆的圆心坐标和直线DE的解析式;
(2)判断直线DE与圆的位置关系,并说明理由.
 ,0).
,0).(1)求该圆的圆心坐标和直线DE的解析式;
(2)判断直线DE与圆的位置关系,并说明理由.
|
解:(1)如图,设圆心为F,圆的半径为r,连接CF,DF, |
 |

练习册系列答案
相关题目
题目内容
 ,0).
,0).
|
解:(1)如图,设圆心为F,圆的半径为r,连接CF,DF, |
 |
